Math Mentor GPT is your go-to AI assistant for demystifying your child's math homework, offering clear explanations and interactive problem-solving guidance.
0

Math Mentor GPT

G0
Never miss a great AI tool
Signup to join 986 AI Modiers
Simplify your child’s math learning journey; ask Math queries, get instant workings
Math Mentor GPT Logo

GPT overview

  • Created by: Chatgpt
Web
Mobile apps
Table of Contents

Math Mentor GPT overview

Math Mentor GPT is an AI-driven tool specifically designed to help parents navigate their children’s math homework.

Unlike general-purpose AI, Math Mentor focuses exclusively on math-related queries, providing clear, step-by-step explanations to demystify complex concepts.

This tool not only assists in solving problems but also enhances understanding by clarifying fundamental concepts in mathematics.

How Math Mentor works

Math Mentor GPT screenshot
  • Understanding specific needs: Math Mentor begins by thoroughly understanding the math problem or concept that a child is facing difficulty with.
  • Tailored guidance: The tool then provides customized, detailed explanations and step-by-step problem-solving assistance.
  • Encouragement for queries: Parents and children are encouraged to ask follow-up questions or seek clarifications, ensuring comprehensive understanding.
  • Educated guesses: In scenarios where specific details might be missing, the Math Mentor GPT makes educated guesses to offer helpful responses, while noting areas where additional information could refine the answer.

Math Mentor GPT real example

Prompt: Give me a refresher course on college-level integration

Sure, here’s the refresher on college-level integration:

Basic concept of integration

  • Integration as antiderifferentiation: Integration is finding the antiderivative or inverse of differentiation. If F'(x) = f(x) , then the integral of f(x) is \int f(x) \, dx = F(x) + C , where C is the constant of integration.
  • Definite and indefinite integrals: An indefinite integral has no bounds and represents a family of functions. A definite integral is evaluated over a specific interval [a, b] and represents the area under f(x) from a to b .

Fundamental theorem of calculus

  • Link between differentiation and integration: This theorem states that if F is an antiderivative of f on [a, b] , then \int_a^b f(x) \, dx = F(b) - F(a) .

Basic integration techniques

  • Power rule: \int x^n \, dx = \frac{x^{n+1}}{n+1} + C , for n \neq -1 .
  • Substitution rule: Used when an integral contains a function and its derivative. If u = g(x) , then \int f(g(x))g'(x) \, dx = \int f(u) \, du .
  • Integration by parts: Based on the product rule for differentiation. \int u \, dv = uv - \int v \, du , where u and dv are functions of x .

Special integrals

  • Integrals of trigonometric functions, exponential functions, and logarithms. For example, \int e^x \, dx = e^x + C , \int \sin(x) \, dx = -\cos(x) + C .

Techniques for complex functions

  • Trigonometric substitution: Useful for integrals involving \sqrt{a^2 - x^2} , \sqrt{a^2 + x^2} , or \sqrt{x^2 - a^2} .
  • Partial fractions: Decomposing a complex rational function into simpler fractions for integration.
  • Improper integrals: Dealing with integrals with infinite limits or integrands with discontinuities.

Applications of integration

  • Calculating areas under curves, volumes of solids of revolution, work done by variable forces, and other physical applications.

Practice and further learning

  • Regular practice with different types of integrals is crucial for mastering these techniques.
  • Revisiting calculus textbooks or utilizing online resources like Khan Academy can deepen your understanding.

Each integration technique has specific contexts and nuances. Working through various examples is beneficial to understand how these techniques are applied in different scenarios. If you have specific types of integrals or problems in mind, feel free to share them!

Starter prompts

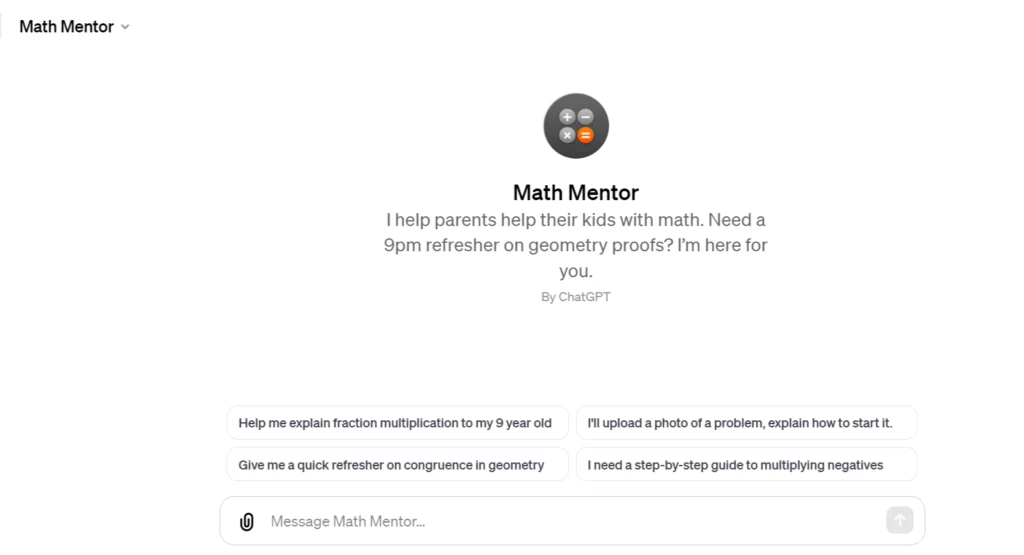
  • Help me explain fraction multiplication to my 9-year-old
  • Give me a quick refresher on congruence in geometry
  • I’ll upload a photo of a problem, explain how to start it.
  • I need a step-by-step guide to multiplying negatives

Math Mentor is designed to make math homework less intimidating and more approachable for both parents and children, ensuring a smoother learning experience in mathematics.

Get Math Mentor GPT

Math Mentor GPT functionalities

Code Interpreter
Dall-E 3
Browsing Experience

Best AI writers

Get 5,000 Words FREE AI Credits

Use our link to generate 5,000 words for free in the next 5 days. ...
Try Koala AI
DEAL

Math Mentor GPT sample prompts

Homework help

My child is struggling with fractions. How can we simplify the fraction 3/9?

Conceptual clarification

My son is confused about the difference between perimeter and area. Can you explain it in simple terms?

Problem solving strategy

My daughter can't figure out this word problem: 'If she has 5 apples and gives 2 to her friend, how many does she have left?' How should we solve this?

Advanced Math topics

Can you break down how to solve quadratic equations? It's a topic my high-schooler is currently studying.

College topics

Give me a rerefresher on Integrations, college level

Prepping for tests

My son is preparing for a math test on Geometry. What are some effective study techniques?

Understanding errors

We tried solving 2x + 3 = 11 but got the wrong answer, ending up with x = 4. Can you show us where we went wrong?

Math games and activities

I'm looking for engaging math games or activities to improve my third-grader's addition skills. Do you have any suggestions?

JetReviews unavailable for this source type

Thanks for taking time to review this tool

Use our link to generate 5,000 words for free in the next 5 days. ...
Try Koala AI
DEAL

Browse more GPTs

Picture of mysson

mysson

AiMode is a blog that focus on using AI tools for improving website copy, writing content faster and increasing productivity for bloggers and solopreneurs.